एमिटर-स्टेबलाइज्ड बीजेटी बायस सर्किट

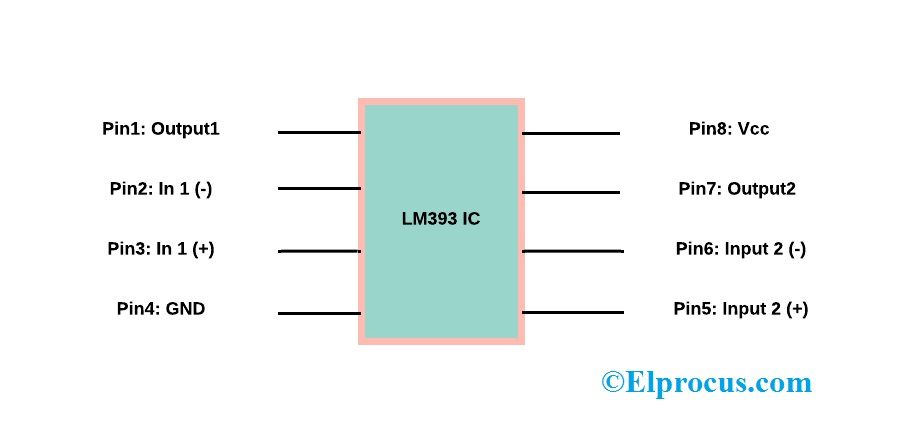
एक कॉन्फ़िगरेशन जिसमें एक द्विध्रुवी जंक्शन ट्रांजिस्टर या BJT को बदलते परिवेश के तापमान के साथ अपनी स्थिरता को बढ़ाने के लिए एक एमिटर रोकनेवाला के साथ प्रबलित किया जाता है, BJT के लिए एक एमिटर स्टेबलाइज्ड पूर्वाग्रह सर्किट कहा जाता है।

हम पहले ही अध्ययन कर चुके हैं कि क्या है ट्रांजिस्टर में डीसी पूर्वाग्रह , अब आगे बढ़ते हैं और सीखते हैं कि BJT DC पूर्वाग्रह नेटवर्क की स्थिरता में सुधार के लिए एक एमिटर अवरोधक का उपयोग कैसे किया जा सकता है।

एमिटर स्थिरीकृत बायस सर्किट को लागू करना

BJT के dc पूर्वाग्रह के लिए एमिटर रेसिस्टर को शामिल करना बेहतर स्थिरता प्रदान करता है, जिसका अर्थ है, dc bias धाराएं और वोल्टेज अधिक निकट होना जारी रखते हैं, जहां वे बाहरी मापदंडों पर विचार करके सर्किट द्वारा तय किए गए थे, जैसे कि तापमान में भिन्नता, और ट्रांजिस्टर बीटा (लाभ),

नीचे दिया गया आंकड़ा एक ट्रांजिस्टर डीसी पूर्वाग्रह नेटवर्क को दर्शाता है जो BJT के मौजूदा निश्चित पूर्वाग्रह विन्यास पर एक एमिटर-स्टेबलाइज्ड बायसिंग को लागू करने के लिए एक एमिटर रोकनेवाला है।

चित्रा 4.17 एमिटर रेजिस्टर के साथ BJT पूर्वाग्रह सर्किट

हमारी चर्चा में हम पहले सर्किट के बेस-एमिटर क्षेत्र के चारों ओर लूप का निरीक्षण करके डिजाइन का विश्लेषण शुरू करेंगे, और फिर सर्किट के कलेक्टर-एमिटर साइड के आसपास लूप की जांच के लिए परिणामों का उपयोग करेंगे।

बेस-एमिटर लूप

हम उपरोक्त बेस-एमिटर लूप को अंजीर 4.18 में नीचे दिखाए गए तरीके से फिर से तैयार कर सकते हैं, और यदि हम आवेदन करते हैं किरचॉफ का वोल्टेज कानून दक्षिणावर्त दिशा में इस लूप पर, हमें निम्नलिखित समीकरण प्राप्त करने में मदद करता है:

+ Vcc = IBRB - VBE - IERE = 0 ------- (4.15)

हमारी पिछली चर्चाओं से हम जानते हैं कि: IE = (β + 1) ख ------- (4.16)

Eq में IE के मान को प्रतिस्थापित करना। (4.15) निम्नलिखित परिणाम प्रदान करता है:

Vcc = IBRB - VBE - (1 + 1) IBRE = 0

अपने संबंधित समूहों में शर्तें रखने से निम्नलिखित पैदावार होती है:

यदि आप हमारे पिछले अध्यायों से याद करते हैं, तो निश्चित पूर्वाग्रह समीकरण निम्न रूप में प्राप्त हुआ था:

यदि हम (4.17) समीकरण के साथ इस निश्चित पूर्वाग्रह समीकरण की तुलना करते हैं, तो हम वर्तमान आईबी के लिए दो समीकरण के बीच एकमात्र अंतर पाते हैं। ((+ 1) आरई।

जब समीकरण 4.17 का उपयोग श्रृंखला आधारित कॉन्फ़िगरेशन को खींचने के लिए किया जाता है तो हम एक दिलचस्प परिणाम निकालने में सक्षम होते हैं, जो वास्तव में समीकरण 4.17 के समान है।

चित्र 4.19 में निम्नलिखित नेटवर्क का उदाहरण लें:

यदि हम वर्तमान IB के लिए सिस्टम को हल करते हैं, तो Eq में समान समीकरण प्राप्त होता है। 4.17। ध्यान रखें कि VBE को उत्सर्जित करने के लिए बेस से वोल्टेज के अलावा, रेसिस्टर RE को एक स्तर पर बेस सर्किट के इनपुट पर फिर से दिखाई दे सकता है। ((+ 1)।

मतलब, एमिटर अवरोधक जो कलेक्टर-एमिटर लूप का एक हिस्सा बनाता है वह दिखाता है ((+ 1) आरई बेस-एमिटर लूप में।

यह मानते हुए कि T ज्यादातर BJT के लिए 50 से ऊपर हो सकता है, ट्रांजिस्टर के उत्सर्जक पर अवरोध बेस सर्किट में काफी बड़ा हो सकता है। इसलिए, हम Fig.4.20 के लिए निम्नलिखित सामान्य समीकरण प्राप्त करने में सक्षम हैं:

री = ((+ 1) आरई ------ (4.18)

भविष्य के कई नेटवर्क को हल करते हुए आपको यह समीकरण काफी आसान लगेगा। दरअसल, यह समीकरण आसान तरीके से समीकरण 4.17 को याद रखने की सुविधा देता है।

ओम के नियम के अनुसार, हम जानते हैं कि एक नेटवर्क के माध्यम से वर्तमान सर्किट के प्रतिरोध से विभाजित वोल्टेज है।
बेस-एमिटर डिज़ाइन के लिए वोल्टेज = है Vcc - VBE

4.17 में देखे गए प्रतिरोध हैं आरबी + आरई , जो के रूप में परिलक्षित होता है () + 1), और परिणाम हमारे पास Eq 4.17 में है।

कलेक्टर-एमिटर लूप

ऊपर दिया गया आंकड़ा कलेक्टर-एमिटर लूप दिखाता है, आवेदन करता है किरचॉफ का नियम संकेतित लूप को दक्षिणावर्त दिशा में, हमें निम्नलिखित समीकरण मिलते हैं:

+ YESTERDAY + आप तोह + ICRC - VCC = 0

एक emitter स्थिर पूर्वाग्रह सर्किट के लिए एक व्यावहारिक उदाहरण को हल करने के रूप में नीचे दिए गए:



उपरोक्त आकृति 4.22 में दिए गए एमिटर बायस नेटवर्क के लिए, निम्नलिखित का मूल्यांकन करें:

1. आईबी
2. I C
3. आप तोह
4. यू
5. तथा
6. आदि
7. वीबीसी

संतृप्ति स्तर का निर्धारण

अधिकतम कलेक्टर वर्तमान जो कलेक्टर बन जाता है संतृप्ति स्तर एक emitter पूर्वाग्रह नेटवर्क के लिए समान रणनीति को लागू करके गणना की जा सकती है जो हमारे पहले के लिए लागू की गई थी फिक्स्ड पूर्वाग्रह सर्किट ।

कलेक्टर के पार एक शॉर्ट सर्किट बनाकर इसे लागू किया जा सकता है और BJT के उत्सर्जक लीड, जैसा कि ऊपर चित्र 4.23 में संकेत दिया गया है, और फिर हम निम्न सूत्र का उपयोग करके परिणामी कलेक्टर वर्तमान का मूल्यांकन कर सकते हैं:

एक एमिटर स्थिर बीजेटी सर्किट में संतृप्ति वर्तमान को हल करने के लिए उदाहरण समस्या:

लोड लाइन विश्लेषण

एमिटर-पूर्वाग्रह BJT सर्किट का लोड-लाइन विश्लेषण हमारे पहले से तय फिक्स्ड-बायस कॉन्फ़िगरेशन के समान है।

एकमात्र अंतर IB का स्तर [जैसा कि हमारे Eq। (4.17)] में पाया गया है) विशेषताओं पर IB के स्तर को परिभाषित करता है जैसा कि निम्न चित्र में दिखाया गया है। 4.24 (IBQ के रूप में दर्शाया गया है)।